В предыдущей статье мы предложили один из возможных критерий качества организации системы.
Рассмотрим
систему, которая представляет собой канал коллективного доступа -
подсистему Z*
и совокупность маршрутизаторов, которые определяют маршруты между
каждой парой абонентов этого канала - подсистему Z**:
Рисунок 1
Предположим,
что в этой системе используется статическая
маршрутизация,
(сеть типа ad
hoc)
то есть маршруты заданы таким образом, что каждой паре абонентов Xi
и Xj
соответствует единственный (непосредственный) маршрут Xi
- Xj.
При таких условиях подсистема Z**
может
находиться в единственном состоянии и, следовательно, H(Z**)=0.
Если в процессе эксплуатации системы, условия радиослышимости в
канале меняются, то H(Z*)>0.
Но подсистема Z**
никак
не реагирует на эти изменения, поэтому H0=H1,
и R=H0-H1=0.
Следовательно, система
предельно неорганизованна.
Допустим
теперь, что подсистема Z**
построена таким образом, что каждому непосредственному маршруту Xi
- Xj,
(кроме маршрутов от Xk)
ставиться в «жесткое» соответствие единственный обходной
маршрут вида Xi
– Xk
- Xj
(Xk
– некая общая «точка доступа», вариант построения
сети
ad
hoc):

Рисунок 2
В
данном случае, энтропия H(Z**)
не может равняться нулю, поскольку подсистема Z**
реагирует на изменение состояний радиолучей – отказ основного
маршрута приводит к использованию обходного маршрута.
Попытаемся оценить
уровень организации такой системы. Действуем поэтапно, в соответствии
с выражениями (3.2) – (3.6).
1)
Будем считать, что вероятность отказа любого радиолуча в канале равна
P.
Тогда
- H(Z*)= -
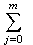 Cmj
{Pj
(1-
P)m-j
log2[
Pj
(1-
P)m-j](3.1)
Cmj
{Pj
(1-
P)m-j
log2[
Pj
(1-
P)m-j](3.1)
где
m
– общее число радиолучей в радиосети, равное
- m = n(n-1)/2(3.2)
n
– общее число маршрутизаторов, включая «точку доступа».
2) Если считать, что
каждый маршрутизатор (кроме точки доступа) выбирает обходной или
основной маршрут с равной вероятностью (по принципу «орёл –
решётка»), то
- H(Z**) = log2 2(n-1)(n-2)/2 = (n-1)(n-2)/2(3.3)
3)
Общее число ситуаций в Z*,
которым соответствует однозначная реакция подсистемы Z**,
ограничено. Действительно (см. рисунок 2), если абонент Xi
намерен передать пакет Xj,
то он воспользуется обходным маршрутом Xi
– Xk
- Xj
только в том случае, если вышел из строя радиолуч Xi
- Xj.
Аналогичным образом, абонент Xj
воспользуется обходным маршрутом
Xj
– Xk
– Xi
только
при отказе радиолуча Xi
- Xj
и т.д.
И
вообще, однозначное соответствие состояния подсистемы Z**состоянию
сети Z*
возможно
только тогда, когда изменения состояний радиолучей будут происходить
только в пределах подмножества E1
(на рисунке 2 эти лучи выделены жирными линиями). Причем в любой из
таких ситуаций P(Zj*|Zk**)=1.
Изменения
структуры вне E1
на поведение системы не влияют, так как любая неудачная попытка
передачи пакета по основному маршруту между любыми XiE1
всегда приводит к передаче того же пакета по обходному маршруту
(независимо от состояния радиолуча Xi
- Xk)
Поэтому:
H
(Z*|Z**)
=
|
(3.4)
|
где
L
= (n-1)(n-2)/2
– число радиолучей в E1.
Графики
зависимостей Н(Z*)
и R
от величины P
(для сети, включающей в себя 8 маршрутизаторов), приведены на рисунке
3.
Рассматривая
эти графики, нетрудно заметить, что рассматриваемая система далека от
совершенства: RН(Z*)
только при весьма надежных каналах связи (P0.05).

Рисунок 3
Но,
при определённых условиях, уровень организации такой системы может
быть признан достаточно высоким. Например, если радиолучи,
связывающие абонентов сети с общей «точкой доступа»,
обладают достаточно высокой надежностью – с вероятностью отказа
=0.15,
а остальные каналы менее надежны – с P0.5,
то
H(Z*)=
-
|
(3.5)
|
H
(Z*|Z**)
=
|
(3.6)
|
и
величина R
сопоставима с H(Z*)
даже при P=0.5
(см. рисунок 4).
Отметим
что в данном случае, степень организации системы увеличивается за
счёт уменьшения энтропии H(Z*),
которое, в свою очередь, достигается за счёт повышения надежности
части радиолучей. Очевидно, что при их стопроцентной надёжности (то
есть при =0)
величина H(Z*)
станет равной R,
и уровень организации в системе может считаться идеальным.
Теперь
предположим, что все элементы системы «сверхнадежны».
Тогда, система, после завершения этапа её развертывания, будет
описываться «железобетонным» графом, который всегда
соответствует заранее известному «замыслу системы».
Очевидно, что такая система не способна к адаптации, (она просто не
нужна), а какая либо информация об её состоянии – бесполезна,
поскольку H(Z*)=H(Z**)=0.
Но, к сожалению, построить такие простые и надёжные сети (тем более,
в полевых условиях) далеко не всегда возможно.

Рисунок 4
По-видимому,
в самоорганизующихся полевых сетях потребуется реализация более
совершенных алгоритмов динамической маршрутизации, основанных на
полном знании текущей топологии сети. К таким алгоритмам, прежде
всего, следует отнести алгоритмы «состояния связей»,
используемые в протоколах типа OSPF.
С
другой стороны, повышение
уровня организации требует наличия и своевременного распространения
достоверной информации
об изменениях топологической структуры сети, которая не может быть
получена без определенного расхода «энергии» или ресурсов
сети. Причём расход
«энергии», необходимый для получения и распространения
такой информации, может с избытком поглотить выигрыш от её
использования.
Например, служебный поток, содержащий полную информацию о структуре
сети связи, может превысить её пропускную способность.
Поэтому,
есть основания предполагать, что высокоорганизованные протоколы
маршрутизации могут найти применение только в высокоскоростных сетях
(типа wi-fi).
В низкоскоростных УКВ-сетях более целесообразна реализация
алгоритмов типа ad-hoc.




