Оценка возможных потерь при возникновении коллизий

Осветив в предыдущей части вопрос оценки зон действия радиосигналов мы переходим к следующему разделу.

Вероятность доставки пакета при абсолютно случайном доступе

Допустим, что устройства, обеспечивающие передачу информации в канал связи, не оснащены какими-либо механизмами, позволяющими избежать коллизий (одновременной работы двух и более передатчиков на одной и той же частоте). Это означает, что любая станция может передавать данные в любое время, и нет никакой гарантии, что эти данные будут успешно доставлены получателю.

Но с другой стороны такая схема доступа, в силу своей простоты, весьма привлекательна и допускается IEEE 802.11. Более того, есть основания предполагать, что она будет устойчиво работать в сетях с малой нагрузкой. Остаётся ответить на вопрос, – с какой?

Особенностью функционирования такой системы является то, что, процесс успешной передачи пакета по любому направлению (X_i, X_j), может быть нарушен при выходе в эфир любой станции, кроме X_i. Вероятность такого события может быть определена с помощью соотношения (3.1):

P(Tij) = 1 - exp (- λ∑ (ij) Tij)

(1)

где

- λ_∑^(ij) – плотность суммарного потока пакетов, поступающих от «конкурентов» станции X_i;

- T_ij - время передачи пакета по направлению (X_i, X_j);

Следует отметить, что формула (1) справедлива только в том случае, если «фоновый» поток λ_∑^(ij) является простейшим, то есть подчиняется закону распределения Пуассона. Однако, ориентация на данный закон может быть обоснована его следующими свойствами:

1. к простейшему потоку системам массового обслуживания иногда приспособиться труднее, и при имитации их работы мы, как бы, ставим систему в более тяжёлые условия;
2. если при исследовании поведения системы мы рассчитываем на этот «тяжёлый случай», то обслуживание реальной системой других случайных потоков с той же плотностью поступления требований будет надёжнее;
3. при сложении нескольких случайных потоков образуется суммарный поток, который по своим характеристикам приближается к простейшему.

Имея значения величин λ_∑^(ij) и T_ij можно вычислить вероятность успешной передачи пакета по любому радиолучу.

Для того чтобы получить эту вероятность следует действовать следующим образом.

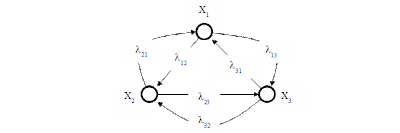
Допустим, что в одну и ту же зону радиослышимости входят три станции, чему соответствует граф, изображённый на рисунке 1:

Рисунок 1

Каждой дуге такого графа (X_i, X_j) может быть поставлен в соответствие поток - λ_ij (будем считать, что такие потоки известны).

Как уже отмечалось, успешное завершение передачи пакета возможно только в том случае, если в интервале T_ij ни одна из «конкурирующих» станций не будет пытаться занять эфир. Вероятность такого стечения обстоятельств может быть определена с помощью соотношения (2):

Pijусп = [1 – P(Tij)] = exp (- λ∑(ij) Tij)

(2)

При этом, величина λ_∑^(ij) будет зависеть от «окружения» передающей и приёмной станций. Для рассматриваемого примера будем иметь:

1. λ_∑⁽¹²⁾ = λ_∑⁽¹³⁾ = λ₂₁ + λ₂₃ + λ₃₁ + λ₃₂ – «фоновый» поток для (X₁,X₂) и (X₁,X₃);
2. λ_∑⁽²¹⁾ = λ_∑⁽²³⁾ = λ₁₂ + λ₁₃ + λ₃₁ + λ₃₂ – «фоновый» поток для (X₂,X₁) и (X₂,X₃);
3. λ_∑⁽³¹⁾ = λ_∑⁽³²⁾ = λ₁₂ + λ₁₃ + λ₃₁ + λ₃₂ – «фоновый» поток для (X₃,X₁) и (X₃,X₂).

Пользуясь соотношением (2), можно найти ориентировочное значение величины P_ij^усп при любом распределении потоков.

Для этого достаточно следующих исходных данных:

1) матрицы Λ^(w)=║λ_ij^(w)║, задающей потоки между всеми парами узлов рассматриваемой зоны «w»;

2) времени передачи пакета - величины T_ij.

Если считать, что все пакеты имеют одинаковую длину и скорости их передачи одинаковы, то величина P_ij^усп может быть представлена в виде функции e^-α, где α=λ_∑T_ij.

График такой функции представлен на рисунке 2.

Рисунок 2

Данный график показывает, что даже относительно небольшой «фоновый» поток, может снизить вероятность успешной передачи пакета до неприемлемой величины. С другой стороны, даже при предельной нагрузке, 37% пакетов могут быть успешно переданы с первой попытки.

Несомненно, что это обстоятельство должно учитываться при подготовке и анализе исходных данных для имитационного моделирования.

Потоки могут быть заданы таким образом, что при моделировании сети могут быть получены «блестящие» результаты.

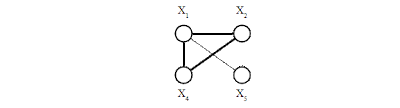
Например (см. рисунок 3), если основная нагрузка на канал ляжет направление (X₁, X₂):

Рисунок 3

а поток α_∑⁽¹⁾ будет отвечать условию (3)

α∑(1) = α21 + α23 + α31 + α32 ≤ 0.02

(3)

то система может оказаться весьма эффективной.

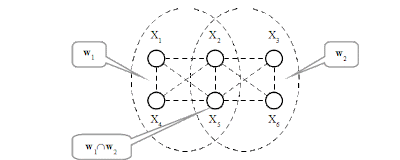
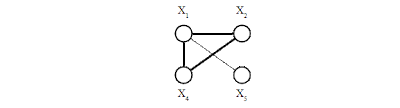
К аналогичным результатам приведёт другой вариант распределения нагрузки, при котором 98% нагрузки будут соответствовать направлениям, инцидентным единственному узлу – X₁ (см. рисунок 4):

Рисунок 4

Но если все величины α_ij будут равны между собой, то канал окажется в наиболее тяжёлых условиях. Причём, с ростом числа абонентов канала, требования к ограничению потока будут всё более и более жёсткими. Поэтому такой режим доступа вряд ли найдёт широкое применение.

Тем не менее, такая схема коллизий понадобится при рассмотрении ситуаций, когда две или несколько станций будут находиться в разных зонах радиослышимости, но будут попадать в зону охвата третьей станции («проблема скрытых станций» ).

Далее мы попробуем оценить вероятность успешного захвата радиоканал в конкурентном окне.

Оценка зон действия радиосигналов

В предыдущей части мы рассмотрели формальное представление сети при моделировании. Теперь же более подробно остановимся на  оценке зон действия радиосигналов.
Для любого типа беспроводной связи передаваемый сигнал рассеивается по мере его распространения в пространстве. Следовательно, мощность сигнала на принимающей антенне будет уменьшаться по мере её удаления от передающей антенны. Причина этого – распространение сигнала по всё большей площади.

Очевидно, что это обстоятельство должно учитываться при составлении графа G=(E,Г), описывающего условия радиослышимости.

Для этого, можно воспользоваться известными моделями распространения радиосигналов. Таких моделей разработано достаточное количество и многие из них можно легко найти в интернете. Согласно одной из моделей, дальность связи – величина D, определяется формулой (1):

D = 10[(FSL / 20) – (33 / 20)lgF]

(1)

где

- F – центральная частота передачи (МГц);

- FSL – потери в свободном пространстве, которые определяется с помощью выражения (2):

FSL = Pt,дБВт + Gt,дБи+ Gr,дБи – Pmin,дБВт – Lt,дБ – Lr,дБ – SOM

(2)

где

- P_t,дБВт – мощность передатчика;

- G_t,дБи - коэффициент усиления передающей антенны;

- G_r,дБи - коэффициент усиления приёмной антенны;

– P_min,дБВт - чувствительность приёмника на используемой скорости передачи;

– L_t,дБ - потери сигнала в коаксиальном кабеле и разъёмах передающего тракта;

– L_r,дБ - потери сигнала в коаксиальном кабеле и разъёмах приёмного тракта.

Все перечисленные величины берутся из паспортных данных используемых приёмных и передающих устройств.

Параметр SOM (System Operating Margin) - учитывает возможные факторы, отрицательно на дальность связи, такие как:

- температурный дрейф чувствительности приёмника и выходной мощности передатчика;

- всевозможные атмосферные явления: туман, снег, дождь;

- рассогласование антенн приёмника и передатчика с антенно-фидерным трактом.

Параметр SOM обычно берётся равным 10 дБ – при инженерных расчётах считается, что такой запас в энергетике связи вполне достаточен.

Теперь представим себе, что пользователю известны расстояния между всеми парами станций – D_ij и характеристики этих станций.

В этом случае, пользователь будет в состоянии оценить возможность радиосвязи между любой парой абонентов – если действительное расстояние D_ij больше соответствующего расчетного значения (см. выражение (1)), то следует считать, что связь между станциями X_i и X_j отсутствует и вероятность существования соответствующего радиолуча – P_ij, приравнивается нулю.

Как уже отмечалось, радиоволна в процессе её распространения в пространстве занимает объём в виде эллипсоида вращения с максимальным радиусом в середине пролёта, который называется зоной Френеля. Естественные преграды - земля, холмы, деревья и искусственные препятствия - здания, холмы и т.д., которые попадают в это пространство, ослабляют сигнал.

Обычно блокирование 20% зоны Френеля вносит незначительное затухание в канал. При блокировании свыше 20% затухание сигнала будет уже заметным, поэтому будем считать, что следует избегать соответствующих мест дислокации станций. Тогда, при подготовке исходных данных для моделирования, можно считать целесообразным следующее предположение: если величина R отвечает неравенству (3)

R > 17,3 [Di Dj / F (Di + Dj)]-2

(3)

где

• D_i – расстояние от антенны станции X_i до самой высшей точки предполагаемого препятствия (см. рисунок 1);
• D_i – аналогичное расстояние от антенны станции X_j;
• F – средняя частота передачи;

то следует считать, что P_ij=0. В противном случае - P_ij=1.

Рисунок 1

В следующей части мы рассмотрим возможные потери пакетов при возникновении коллизий в канале коллективного доступа.

Формальное представление текущего состояния сети при моделировании.

Итак, рассмотрев основные особенности моделирования протоколов IEEE 802.11, мы переходим к формальному описанию моделируемой сети связи.

Описание структуры сети

Очевидно, что при изучении и имитации процессов движения пакетов по сети, необходимо учитывать, по крайней мере, следующие факторы:

1) распределение радиочастот;

2) изменчивые условия радиослышимости;

3) и, наконец, распределение потоков информации, которое может изменяться при адаптации системы к возникшим ситуациям.

Совокупность радиочастот и потенциальная возможность их использования теми или иными станциями может быть описана гиперграфом H=(Е,W), вершины которого соответствуют узлам сети, а подмножества w_k  W - используемым частотам. Описание гиперграфа H=(E,W) может быть задано либо в форме списков w_k={Xi₁, Xi₂, . . . , Xi_N}, либо в виде матрицы инциденций ║S_ik║ элемент которой

Например, изображённый на рисунке 1 гиперграф может быть представлен в виде матрицы ║S_ik║, представленной на рисунке 2:

Рисунок 1

	w1	w2
X1	1	0
X2	1	1
X3	0	1
X4	1	0
X5	1	1
X6	0	1

Рисунок 2

Элементы X_iw_1w₂ соответствуют узлам, которые могут воспользоваться как частотой w₁, так и частотой w₂. 

Условия радиослышимости могут быть описаны неориентированным графом G=(E,Г), вершины которого соответствуют узлам сети. Вершины, которые соответствуют парам слышащих друг друга абонентов, соединяются ребром.

Следует подчеркнуть, что в такой граф включаются далеко не все потенциально возможные соединения. Например, изображенному на рисунке 1 гиперграфу может соответствовать граф, изображённый на рисунке 3:

Рисунок 3

Граф G=(E,Г) может быть описан матрицей смежности - A=║A_ij║. Число строк и столбцов такой матрицы должно соответствовать числу узлов в сети. Элементы матрицы ║A_ij║ отражают структуру графа G=(E,Г), соответствующего текущему состоянию сети:

Например, изображённому на рисунке 3 графу будет соответствовать матрица, показанная на рисунке 4:

	X1	X2	X3	X4	X5	X6
X1		1	0	1	0	0
X2	1		1	1	1	1
X3	0	1		0	0	0
X4	1	1	0		0	0
X5	0	1	0	0		0
X6	0	1	0	0	0

Рисунок 4

Имитация процессов отказов/восстановлений радиолучей

Содержимое матрицы A_ij периодически изменяется, что имитирует процесс изменений условий радиослышимости.

Эти вероятности могут быть заданы в виде матрицы P=║P_ij║, каждый элемент которой, соответствует потенциально возможному радиолучу, заданному гиперграфом H=(Е,W), а значение этого элемента – вероятности существования этого радиолуча.

При наличии такой матрицы, генерация ситуаций, связанных с отказами/восстановлениями радиолучей может осуществляться с помощью следующего алгоритма:

1) матрица A=║A_ij║ «обнуляется»;

2) поочерёдно просматриваются элементы матрицы P, отвечающие условию (1):

i < j

(1)

3) если просматриваемый элемент отвечает условию (2)

0 < Pij < 1

(2)

то

- генерируется случайное число - x, в интервале {0, …, 1};

- проверяется условие (3):

Pij  x

(3)

и, если условие (3) выполняется, то в граф G=(E,Г) добавляется две дуги - (X_i,X_j) и (X_j,X_i).

Отметим, что, при выборке ситуаций, изменения структуры сети не считаются необратимыми – генерация новых ситуаций всегда опирается на заданное описание сети – гиперграф H=(Е,W).

Приведённый алгоритм может быть проиллюстрирован следующим примером. Рассмотрим заданный пользователем фрагмент сети, который представлен на рисунке 5:

Рисунок 5

Допустим, что станции X₁, X₂ и X₄ не меняют своей дислокации и связь между ними устойчива, а станция X₅ может потерять связь с любой из этих станций, поскольку место её дислокации выбрано неудачно.

Этому фрагменту может быть поставлена в соответствие матрица P, которая представлена на рисунке 6.

	X1	X2	X4	X5
X1		1	1	0.5
X2	1		1	0.8
X4	1	1		0
X5	0.5	0.8	0

Рисунок 6

Предположим теперь, что при выполнении приведённого алгоритма, датчик случайных чисел сформировал следующие значения x:

1. при рассмотрении элемента P₁₅ – число x=0.4;
2. при рассмотрении элемента P₂₅ – число x=0.6.

При таких значениях x матрица A=║A_ij║ будет иметь вид, представленный на рисунке 7, а соответствующий граф G=(E,Г) будет иметь вид, представленный на рисунке 8:

	X1	X2	X4	X5
X1		1	1	1
X2	1		1	1
X4	1	1		0
X5	1	1	0

Рисунок 7

Рисунок 8

(Обратим внимание на то, что при рассмотрении величин P_ij=1 и P_ij=0, случайные числа x не играют никакой роли – если P_ij=1, то в граф G=(E,Г) всегда будет включено соответствующее ребро, и наоборот - если P_ij=0, то вершины X_i и X_j не будут считаться смежными).

Очевидно, что при использовании рассматриваемого алгоритма (при иных значениях x), может быть построены четыре варианта графа G=(E,Г) - на рисунке 8 приведён только один из них. Но возможны ещё три варианта:

1. вариант, представленный на рисунке 9 (вероятность появления такой ситуации - P₁₅ (1-P₂₅ ) = 0.1):
   

   

Рисунок 9

2. вариант, представленный на рисунке 10
    (вероятность появления ситуации - P₂₅ (1-P₁₅) = 0.4):
   

   

Рисунок 10

3. и, наконец, вариант, представленный на рисунке 11 (вероятность появления такой ситуации - (1-P₂₅ ) (1-P₁₅ ) = 0.1):
   

   

Рисунок 11

2.3. Таким образом, в результате имитации процессов отказов/восстановлений радиолучей, мы можем получить любые структуры, и, имея граф G=(E,Г) - установить возможность успешной доставки пакетов по всем заданным маршрутам. Для этого необходимо иметь план распределения нагрузки в сети, который определён процедурами маршрутизации.

Этот план может быть представлен в виде множества суграфов G_a=(E,Г_a), каждый из которых соответствует конкретному узлу-получателю - .X_a.

Например, для представленного на рисунке 1 примера сети, суграф G₁=(E,Г₁) может иметь вид, представленный на рисунке 12:

Рисунок 12

Такой суграф может быть описан в виде матрицы смежности – M^(a) =║M_ij^(a)║, элемент которой

Например, представленный на рисунке 12 суграф может быть оформлен в виде матрицы, которая показана на рисунке 13:

	X1	X2	X3	X4	X5	X6
X1		0	0	0	0	0
X2	1		0	0	0	0
X3	0	1		0	0	0
X4	1	0	0		0	0
X5	1	0	0	0		0
X6	0	0	0	0	1

Рисунок 13

Имея матрицы M^(a) =║M_ij^(a)║ и A=║A_ij║, можно построить результирующую матрицу B^(a)=║B_ij^(a)║ элементы которой определяются конъюнкцией элементов M_ij^(a) и A_ij, то есть соотношением (4):

Bij(a) = Mij(a)  Aij

(4)

Такая матрица позволит установить «реальные» маршруты пакетов к получателю X_a и перечень узлов, в которых эти пакеты будут теряться.

Одной из ключевых моделей при моделировании беспроводных систем связи, является модель распространения радиосигнала и оценка зон действия этих сигналов в рамках выбранной модели распространения.